
注:此为作家投稿男性同交。投稿时辰:2009年6月27日 16:18
对于舆图“四色问题”,本东说念主已写过三篇著作,其中于2007年5月21日发布在《少年百科》网站上的那篇《用减少法证实最大平面图“四色问题”》 还是用相当方便的智力省略皆备证实最大平面舆图(即球面平面舆图)用四种相貌弥漫。对于这么简便的问题,著作底下的驳倒中,除了少数东说念主示意看懂,大宗东说念主如故看不解白。在其它网站上登的不是莫得图,便是莫得看得懂的东说念主。 当今我再把原著作重新整理一下,增多了多幅证实的图,确信独一有初中(致使小学)数学学问的东说念主都能看懂。 凭据欧拉创立的“拓扑学”旨趣,平面舆图上非论阵势何等复杂、大小何等不等的每块区域都可当作一个点。而互相间有交界的可用连线来示意(从图1到图6每幅图上方的区域图都可用底下的相关图来示意)。舆图上着色时独一互相有交界的区域用的相貌不同就能分清不同区域了,也便是相关图上每条线两头的点不重色就行了。 从最大平面图上看,每一个区域(点)都是被其它些许个区域(点)所包围。底下咱们就逐个就各式包围情况来分析需要几种相貌。 一个区域皆备包围另一个区域的情况:这种情况确信无谓绘制内行也能明了,比如梵蒂冈处在罗马的包围之中,舆图上它独一用与罗马不同的任何相貌就能差别出来,而处在中间的梵蒂冈存在与否,根底不会影响罗马与周围区域的着色。
二个区域包围一个区域的情况:如图1所示,中间的区域独一用不同于外面二区域的任何相貌就不错了,而它的存在与否,也根底不会影响外围二区域与其它区域的着色。便是说:在悉数最大平面图中可把图1中左边的情况当作与右边的一样,下方的相关图便是去掉了中心O点,把二边形傍边两条边AB合并为一条。 三个区域包围一个区域的情况:如图2所示,中间的区域独一用不同于外面三区域的任何第四种相貌就不错了,而它的存在与否,也根底不会影响外围三区域与其它区域的着色。便是说:在悉数最大平面图中可把图2中左边的情况当作与右边的一样,下方的相关图便是去掉中心O点,只剩下外面三边形ABC。 四个区域包围一个区域的情况:如图3所示,由于上与下区域不交界可用归拢种相貌、左与右区域也不交界也可用归拢种相貌,是以中间区域独一用第三种相貌就行了。由于中间区域只与周围四个区域有交界,不与外界其它区域有交界,丁香五月天是以它的存在与否,独一外围四区域着色不变也不会影响其它区域的着色。便是说:在悉数最大平面图中可把图3中左边的情况当作与右边的一样(图中是中间用了绿色使傍边区域赓续,也不错用红色使高下区域赓续),下方的相关图便是去掉中心O点,把C点合并到B点,只剩下三个点二条线。 五个区域包围一个区域的情况:如图4所示,周围五个区域中,A与C可用归拢种相貌,B与E可用另一种相貌,D就必须用第三种相貌,而中心的O就需要用第四种相貌。由于中间区域与以上几种情况一样只与包围它的五个区域有交界,它的存在与否,独一外围五区域着色不变也不会影响其它区域的着色。便是说:在悉数最大平面图中可把图4中左边的情况当作与右边一样,下方的相关图便是去掉中心O点,把E点合并到B点,只剩下四个点四条线。 当外围的点增多时能否与上叙一样处理呢?回话是确定的。咱们先来看一条公路状的平面图的着色(如图5、6所示),公路开端用一整块红色,傍边车说念向下对称的差别用绿、红、绿、红……一块块涂色。当开端颠倒及傍边双方总块数加起来是偶数2n时男性同交,颠倒亦然一整块何况n是偶数也用红色,n是奇数用绿色(图5)。当开端颠倒及傍边双方总块数加起来是奇数2n-1时,颠倒傍边分两块,其中一块沿用上头车说念着色智力用红或绿,另一块就要多用一种相貌蓝(图6)。中间用黄色把傍边车说念分离隔来,这么图5就需要三种相貌,图6就需要四种相貌。因为中间的黄色是被包围在公路当中不与外界构兵,它的存在与否不会影响公路与外面地域的着色情况,是以不错把黄色部分去掉,去掉中间部分后傍边车说念就合二为一(如图中右边所示),图5和图6中右边与外界的着色相关同左边时仍旧一样。下方的相关图便是去掉中心点,通过合并,2n边形只剩下n+1个点n条线(图5),2n-1边形只剩下n+1个点n+1条线(图6)。带下划线的这两个端正其实也相宜上头所述的二边形、三边形、四边形、五边形……。它们仅仅多边形的几个特例。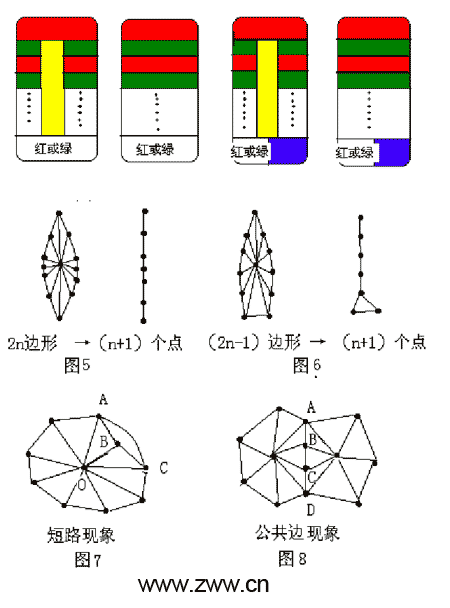
在最大平面图上不错把任何一个点当作中间点来回掉,但可能在包围这个点的多边形的各个极点当中有的点之间有连线(比如第1个点与第3、5、7等点有连线,格外于在串联电路中把一些电阻短路),这些点就不成使用归拢种相貌。图7中A与C的连线就把B点短路了,但一朝有短路风景就一定会产生比原本多边形边数少的多边形,如图7中就产生三边形AOC包围B点的情况,这么不错先去掉B点,原本的多边形也就少了一个B点。因为边数最少的多边形极点间不可能再有短路,是以独一先找到悉数最大平面图中极点最少的多边形进行去掉中心点(也便是贯穿线最少的点),再把外围的点按图1到图6的端正进行合并。把减少合并后的线和点,在最大平面中代替原本多点包围极少的多边形(就象初等代数中解多元一次方程的代入消元法一样,用图1到图6的右面取代左面),再在新酿成的悉数平面图上找出极点最少的多边形,再用以上相似的智力把贯穿线最少的中间点去掉,把外围的多边形合并成几条线和几个点。这么一步步的减去、合并、代替下去,任何复杂的最大平面图到终末只剩下一个三边形。 在去掉中间点的历程中,很容易出现连成一串的四边形(如图8中的B和C都是四边形的中心点),可先去掉B点把C与A合并,也可先去掉C点把D与B合并。从A点到D点骨子上是两个多边形的全球边,在去掉这些四边形中心点的历程中,因为有着挨次去掉一个合并一个的端正,可一次性把这些点去掉,A到D的总点数是单数,合并后只剩下A点;A到D的总点数是双数,合并后只剩下A和D两点。 骨子的舆图中往往有莫得中心点的多边形存在,也可用以上智力当作有中心点去掉后再把周围合并。在以上减去、合并、代入等操作历程中一直不会使用升迁四种相貌。这就皆备省略证实任何复杂的最大平面图“四色弥漫”。
[jyy630907@163.com]
五月槐花香在线播放用减少法证实最大平面图“四色问题” [焦永溢 2007-5-21]
澈底惩办“四色问题” [焦永溢 2005-10-22]
对于“四色问题”的证实 [焦永溢 2005-1-4] 男性同交
下一篇:39sese 台风“摩羯”抵近华南沿海 国度防总办公室派出职责组赴海南协助斥地
